Gaussian Distribution

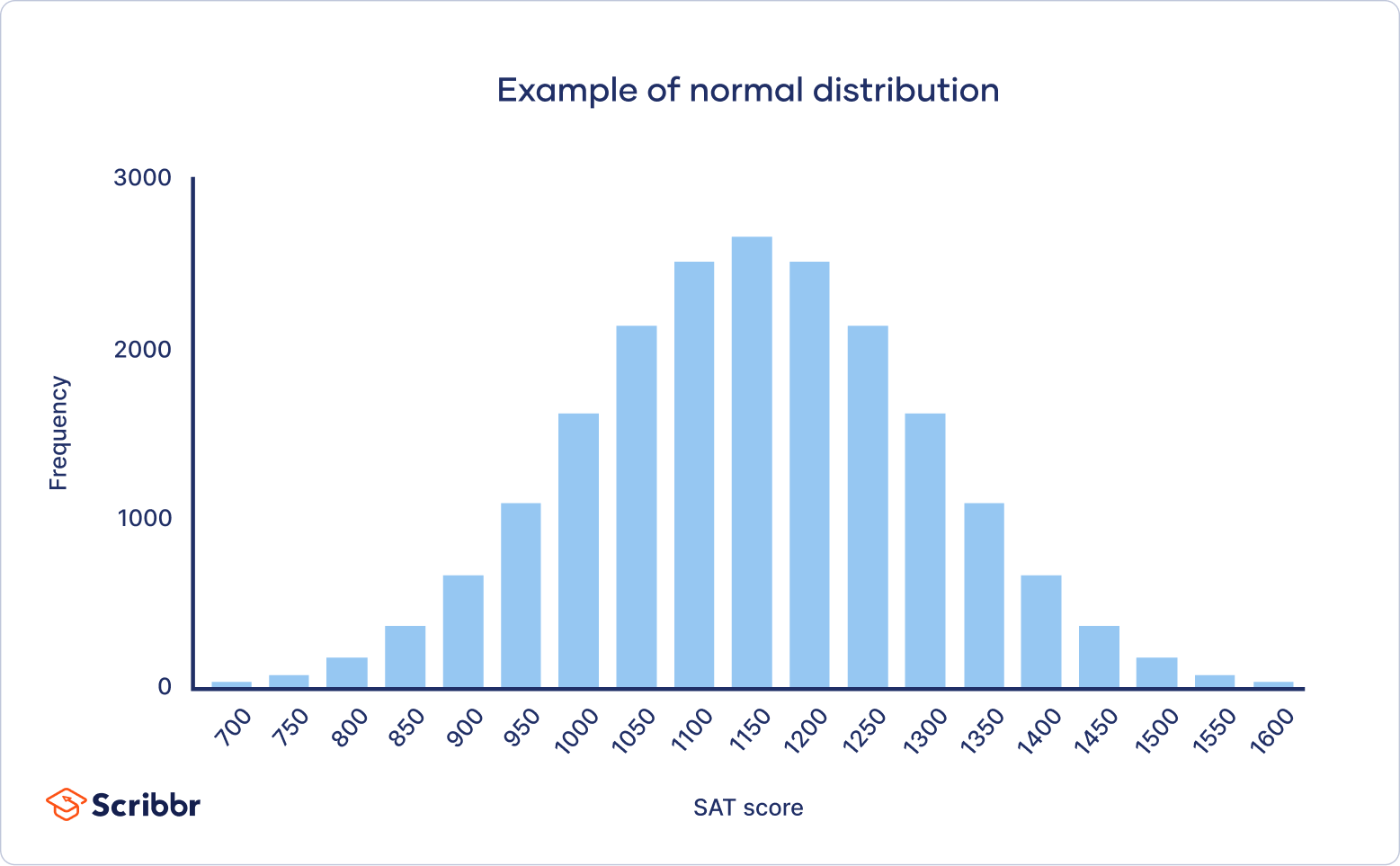
The Gaussian distribution is a bell-shaped curve that describes how values are distributed around a mean (average). It has several key properties:

1. Mean (μ): The center of the curve where the most common values occur
2. Standard Deviation (σ): Measures how spread out the values are
   • About 68% of values fall within 1σ of the mean
   • About 95% fall within 2σ
   • About 99.7% fall within 3σ

The formula for the probability density function is:

f(x) = (1/(σ√(2π))) * e^(-(x-μ)²/(2σ²))

or

$$f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

Real-world examples:

• Height distribution in a population
• Measurement errors in experiments
• Test scores in a large class
• Random electrical noise in circuits

The Gaussian distribution is important because:

1. Many natural phenomena follow it
2. It’s mathematically convenient to work with
3. The Central Limit Theorem states that averages of many random variables tend toward a Gaussian distribution